We use Kepler's Third Law, which states that
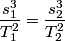 for any two bodies orbiting the same mass. Here, we let 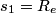 be the radius of the earth, be the radius of the earth, 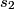 be the radius of the synchronous satellite orbit, be the radius of the synchronous satellite orbit, 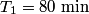 be the period of the hypothetical satellite orbiting at sea level, and be the period of the hypothetical satellite orbiting at sea level, and 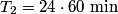 be the period of the synchronous satellite. Then be the period of the synchronous satellite. Then 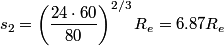 Thus, answer (B) is correct. |